External functions and Grace
Grace, known also by its command xmgrace, is a program for creating scientific graphs and is also capable of common data analysis tasks like fitting, Fourier transformation, etc. Unfortunately, the built-in mathematical functions are in some cases not enough. The Grace authors added therefore a mechanism to facilitate the loading of external functions.
This post basically follows the Grace User’s Guide part about DL Modules, just using a different example.
In NMR it is common to describe the magnetization build-up or decay with a Kohlrausch-William-Watts (KWW) function. Essentially it is an exponential function with stretching parameter \(\beta\):
\[S(t)=e^{-\left(\frac{t}{T_1}\right)^{\beta}}\]In \(test\) xmgrace syntax the fit function can then be described with:
exp(-(x/A0)^A1)
A two step magnetization decay can be described with the following function:
\[S(t)=M_0\left[ \left(1-f\right)\cdot e^{-\left(\frac{t}{T_{1,2}}\right)^{\beta_1}}+f\cdot e^{-\left(\frac{t}{T_{1,2}}\right)^{\beta_2}}\right]\]In xmgrace syntax this becomes:
A0*( (1-A1)*exp(-(x/A2^A3) + A1*exp(-(x/A4)^A5) )
with A0 = \(M_0\) the magnetization amplitude, A1 = \(f\) the component part, A2, A4 = \(T_{1,1}\), \(T_{1,2}\) the time constants and A3, A5 = \(\beta_1,\,\beta_2\) the stretching parameters.
Now it would be nice to access such a long function directly instead of typing/copying it every time we need it. This is now the point were loading external functions comes in to play.
What we need (according to the Grace manual):
- shared library compiled with position independent code (PIC)
- the function you want to use must map to one of the following Grace types and return a double (see table below)
- if the function does not correspond to any of the Grace types you need to create wrapper of the function.
| Grace type | Description |
| f_of_i | a function of 1 int variable |
| f_of_d | a function of 1 double variable |
| f_of_nn | a function of 2 int parameters |
| f_of_nd | a function of 1 int parameter and 1 double variable |
| f_of_dd | a function of 2 double variables |
| f_of_nnd | a function of 2 int parameters and 1 double variable |
| f_of_ppd | a function of 2 double parameters and 1 double variable |
| f_of_pppd | a function of 3 double parameters and 1 double variable |
| f_of_ppppd | a function of 4 double parameters and 1 double variable |
| f_of_pppppd | a function of 5 double parameters and 1 double variable |
Simple case
Let’s assume for the beginning we want to use the digamma function from the GNU Scientific Library (GSL). It is generally defined as:
\[\psi(x) = \Gamma'(x)/\Gamma(x)\]The actual GSL function is gsl_sf_psi (double x) and returns a double, and we want to call it directly in Grace.
Assuming the GSL library is installed in the standard way (apt-get or rpm) so that it is in the default search path for dynamically loaded libraries, there is nothing more to do than starting Grace with:
xmgrace -pexec \
'USE "gsl_sf_psi" type f_of_d from "/usr/lib/libgsl.so.0" alias "psi"'
You can now access the \(\Psi(x)\) function with psi(x) anywhere in Grace. In this way you can get access to all of the special functions offered by the GSL, from the manual:
The library includes routines for calculating the values of Airy functions, Bessel functions, Clausen functions, Coulomb wave functions, Coupling coefficients, the Dawson function, Debye functions, Dilogarithms, Elliptic integrals, Jacobi elliptic functions, Error functions, Exponential integrals, Fermi-Dirac functions, Gamma functions, Gegenbauer functions, Hypergeometric functions, Laguerre functions, Legendre functions and Spherical Harmonics, the Psi (Digamma) Function, Synchrotron functions, Transport functions, Trigonometric functions and Zeta functions.
Of course you can use any other math library, or you can create your own, which we will do in the next section.
Our own code
The bi-exponential decay can be coded in C. Here is the content of an implementation of the KWW function and the bi-exponential function discussed above:
#include <math.h>
double kww(double signal, double T1, double beta, double t) {
double y;
y = signal*exp(-pow(t/T1,beta));
return y;
}
double biexp(double f, double T11, double beta1, double T12, double beta2, double t) {
double y;
y = kww(1-f, T11, beta1, t) + kww(f, T12, beta2, t);
return y;
}As you can see we define first the KWW functions, and use them to define our bi-exponential function. Note also that I do not use the \(M_0\) parameter. This is due to the fact that there can be not more than 5 parameters and one variable (see the table about Grace types).
In order to use this library we need to compile it first as a shared library (-shared) with position independent code (-fPIC) and, because we use math functions, we also need to link it to libm.so (-lm):
gcc -O2 -shared -fPIC -lm xmgrace_functions.c \
-o xmgrace_functions.so
Then we need to start Grace with the following parameters (in the same directory 1):
xmgrace -pexec \
'USE "biexp" type f_of_pppppd from "xmgrace_functions.so" alias "biexp"'
This tells Grace to use the biexp function which takes 5 parameters and 1 variable (f_pppppd) from the xmgrace_fucntions.so library and provide it to the user as a function with name biexp.
Finally, here is an example where I used the biexp function to calculate a decay:
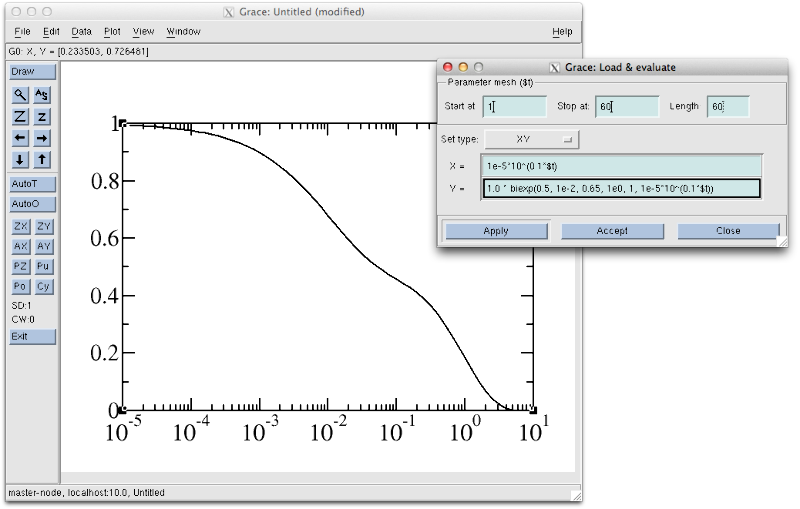
If you use this function on a regular basis it is better to put the Grace command in your ` ~/.grace/gracerc.user`. This file is read upon every start of Grace and will provide your custom function in every instance, ready to be used. Here is for example an excerpt of my grace user file:
DEVICE "PNG" DPI 600
DEVICE "PNG" OP "transparent:on,compression:6"
USE "biexp" type f_of_pppppd from "xmgrace_functions.so" alias "biexp"
Do not forget to change/set your LD_LIBRARY_PATH.
Unfortunately this is not supported on Mac OS X, but it works nice on Linux. The example above is tested and worked on Debian Wheezy.
-
You can start Grace anywhere, but you have to make sure it can find your library. One way is to set the
LD_LIBRARY_PATHvariable to the proper directory. How to do this depends on your shell (BASH, TCSH, DASH,…) ↩